BspNr: F0010
|
Themenbereich
|
Differential- und Integralrechnung |
|
Ziele
|
vorhandene Ausarbeitungen
|
|
|
TI-92 (F0010a) (146 KB)
Mupad-Notebook (F0010b) (60 KB) |
| Analoge Aufgabenstellungen - Übungsbeispiele |
F0011, F0012 |
| Lehrplanbezug (Österreich): |
8. Klasse |
| Quelle: Dr. Thomas Himmelbauer |
Formel 1 - Rennen am Tiongring
Angabe
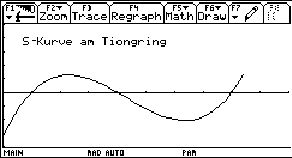
Die Start-Ziel Gerade des Tiongrings geht in eine gefürchtete S-Kurve über. Die Funktion
s(t)=(
xt1(t)=t
yt1(t)=
(t−1)⋅(t−4)⋅(t−8)
10
)
beschreibt die Bahnkurve eines Boliden in diesem Bereich für den Zeitraum t = 0 s bis t = 8,5 s. Die Größe der Einheit beträgt 25 m.
Fragen:
Während des Rennens wurden bei der TV-Übertragung vom Kommentator Reinz Hüller folgende Aussagen gemacht.
- Die Länge dieses Streckenabschnittes beträgt 2 km.
- Die Durchschnittsgeschwindigkeit in diesem Bereich beträgt 200 km/h.
- Die Höchstgeschwindigkeit in diesem Bereich beträgt 400 km/h.
- Die kleinste Geschwindigkeit in diesem Bereich beträgt 90 km/h.
- Die größte Zentripetalbeschleunigung beträgt das Fünffache der Erdbeschleunigung g = 9,81 m/s2.
- Überprüfe diese Aussagen durch eigene Berechnungen.
- Die Zentripetalbeschleunigung an ist sowohl mit Hilfe der Formel
a
n
=
(
v
a
)
2
ρ
als auch als Normalkomponente der Beschleunigung zu berechnen.
v
a
... absoluter Betrag der Geschwindigkeit.
ρ ... Krümmungsradius
ρ(x)=|
(1+
f
′
(x)
2
)
3
2
f
″
(x)
|
... ist der Radius des Krümmungskreises an der Stelle x
- (wenn die Kurve in der Form y = f(x) vorliegt)
© ACDCA, 2002 - Beispielsammlung, Projekt "Technologie im Mathematikunterricht"
Kontakt-E-Mail: acdca@pinoe-hl.ac.at