BspNr: E0110
|
Themenbereich
|
Quadratische Funktionen, Extremwertbeispiele |
|
Ziele
|
vorhandene Ausarbeitungen
|
- Anwendung der beschleunigten Bewegung
- Parameterfunktion
|
TI-92 (E0110a) (81 KB) |
| Analoge Aufgabenstellungen - Übungsbeispiele |
E0111, E0112 |
| Lehrplanbezug (Österreich): |
5. Klasse |
| Quelle: Dr. Thomas Himmelbauer |
Schiefer Wurf ohne Luftwiderstand
Angabe
Für den schiefen Wurf ohne Luftwiderstand gilt als gleichmäßig beschleunigte Bewegung folgendes Weg-Zeit-Gesetz:
s(t)
⟶
=
s
0
⟶
+
v
0
⟶
⋅t+
a
⟶
2
⋅
t
2
Dabei ist
s
0
⟶
=(
0
h
0
)
der Ort mit der Höhe h0, wo der Abschuss zum Zeitpunkt t = 0 erfolgt,
v
0
⟶
=(
v⋅cos(wi)
v⋅sin(wi)
)
ist die Geschwindigkeit zum Zeitpunkt t = 0, v ist die Größe der Geschwindigkeit,
wi ist Abschusswinkel und
a
⟶
=(
0
−g
)
ist die Erdbeschleunigung mit g = 9,81 m/s2.
Damit ergibt sich folgende Bewegungsgleichung:
s(
t
)
⟶
=(
v⋅cos(wi)⋅t
h
0
+v⋅sin(wi)⋅t−
9.81
2
⋅
t
2
)
Zeichnung: |
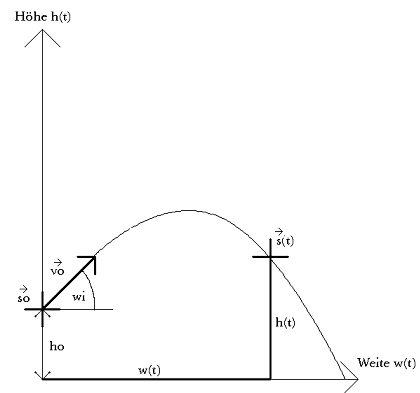 |
Fragen:
- Berechne für gegebene Abschusshöhe h0 = 0 m, Abschussgeschwindigkeit v = 30 m/s und Abschusswinkel
wi = 30° die Wurfdauer, Wurfweite und größte Wurfhöhe! Überprüfe dabei über die graphische Darstellung der Bewegung deine Berechnung!
- Berechne für Abschusshöhe h0 = 0 m und Abschussgeschwindigkeit v = 30 m/s den Abschusswinkel wi, mit dem die größte Wurfweite erzielt wird!
- Berechne für Abschusshöhe h0 = 100 m und Abschussgeschwindigkeit v = 30 m/s den Abschusswinkel wi, mit dem die größte Wurfweite erzielt wird!
© ACDCA, 2002 - Beispielsammlung, Projekt "Technologie im Mathematikunterricht"
Kontakt-E-Mail: acdca@pinoe-hl.ac.at

