Angabe und Fragen:
- Ende 1990 (t = 0) waren gerade einmal ca. 180 Viren bekannt. Ende 1998 (t =8) waren schon ca. 18 500 Computerviren bekannt. Berechnen Sie die Gleichung der Wachstumsfunktion in der Form y(t) = y0 . ek.t und geben Sie die Gleichung an.
- Um wie viel Prozent wächst die Anzahl der Viren pro Jahr?
- In welchem Jahr hat sich die Anzahl der Viren verzehnfacht?
Gehen Sie vom Jahr 1990 aus. (Jahreszahl angeben) - In welchem Jahr gibt es (nach diesem Modell) 20 000 Viren?
Wie viele bekannte Viren wird es (nach diesem Modell) bis Ende 2005 insgesamt weltweit geben? - Berechnen Sie die Gleichung der Wachstumskurve mit exponentieller Regression und geben Sie die Wachstumsgleichung an. Verwenden Sie zur Berechnung die Daten der gegebenen Tabelle.
- Um wie viel Prozent wächst die Anzahl der Viren pro Jahr nach dieser Art der Berechnung?
- Berechnen Sie die Gleichung der Wachstumsfunktion mit logistischer Regression und geben Sie die Wachstumsgleichung an.
Skizzieren Sie die Kurve des logist. Wachstums der Virenanzahl. Verwenden Sie zur Berechnung die Daten der gegebenen Tabelle. - In welchem Jahr gibt es (nach dem Modell des logistischen Wachstums) 20 000 Viren?
Wie viele bekannte Viren wird es (nach diesem Modell ) bis Ende 2005 insgesamt weltweit geben? - In welchem Jahr ist die Zunahme der Zahl der Computerviren (nach dem Modell des logistischen Wachstums) maximal? (Jahreszahl angeben)
Computerviren stellen für IT-Anwender eine große Gefahr dar. Die Anzahl der bekannten Computerviren ist in den letzten zehn Jahren weltweit exponentiell gewachsen. (Modellannahme!)
Berechnung mit Regression:
Gehen Sie von exponentiellem Wachstum aus.
Gehen Sie in einer zweiten Modellannahme von einem logistischen Wachstum der Zahl der Viren aus.
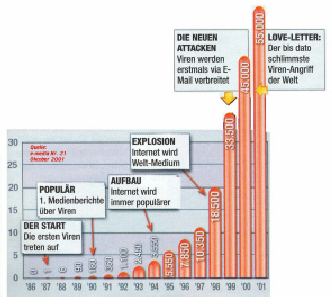
| Ende des Jahres | t | Gesamtzahl der Viren |
| 90 | 0 | 180 |
| 91 | 1 | 360 |
| 92 | 2 | 1100 |
| 93 | 3 | 2450 |
| 94 | 4 | 3550 |
| 95 | 5 | 5550 |
| 96 | 6 | 7850 |
| 97 | 7 | 10350 |
| 98 | 8 | 18500 |
| 99 | 9 | 33500 |
| 2000 | 10 | 45000 |
| Sept. 2001 | 10,75 | 55000 |