BspNr: A0412
Themenbereich |
|
Analytische Geometrie, Ellipse |
|
|
Ziele
|
vorhandene Ausarbeitungen
|
|
|
TI-92 und Cabri (A0412a) (126 KB) |
| Analoge Aufgabenstellungen - Übungsbeispiele | |
| Lehrplanbezug (Österreich): | 6. Klasse |
| Quelle: Franz Hauser (nach Idee von Josef Böhm: Von Pol zu Pol, von Sprung zu Sprung) | |
Angabe und Fragen:
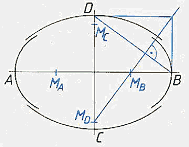
Zeichne mittels "Dynamischer Geometrie"-Software die Ellipse mit a = 5, b = 3 (1.Hauptlage) und konstruiere Scheitelschmiegkreise mit Hilfe von Streckensymmetralen (verwende dazu die Scheitelpunkte und "nahe gelegene" Ellipsenpunkte).
Führe diesen Vorgang analytisch durch und gib die Gleichungen der Scheitelschmiegkreise an.
| Zeige, dass die in vielen Lehrbüchern angegebene Konstruktion (Abbildung) zum gleichen Ergebnis führt. |  |
© ACDCA, 2002 - Beispielsammlung, Projekt "Technologie im Mathematikunterricht"
Kontakt-E-Mail: acdca@pinoe-hl.ac.at