Programmierkurs 

---

Die Loop...EndLoop-Schleife

Mit diesem Schleifentypus wird eigentlich eine Endlosschleife erzeugt, da der Befehl Loop keine Argumente besitzt. Eine derartige Schleife ist also unbedingt mit dem Befehl Exit zu versehen, der wie bei der FOR-Schleife, das Beenden der Schleife ermöglicht. Die genaue Syntax dieses Befehls lautet:
 

Fußgesteuerte Schleife	Kopfgesteuerte Schleife
Loop   Anweisungen    If logische Bedingung     Exit EndLoop	Loop   If logische Bedingung     Exit Anweisungen EndLoop
Hier werden die Anweisungen innerhalb der Schleife mindestens einmal ausgeführt.	Hier wird die Schleife nur ausgeführt, wenn die logische Bedingung wahr ist.

 

Solltest du dennoch einmal eine ungewollte Endlosschleife progammiert haben, kannst du das Programm jederzeit mit der -Taste beenden.

 

Beispiel 9 ("Primzahltest mittles Loop...EndLoop") Formuliere den Primzahltest mit Hilfe einer Loop-Schleife. Sollte die zu testende Zahl keine Primzahl sein, soll weiters noch der kleinste echte Teiler angezeigt werden.

Bei einer Loop-Schleife existiert keine Laufvariable, also müssen wir eine Zählervariable einführen, die bei jedem Schleifendurchlauf um zwei erhöht wird. Da der Wert dieser Zählervariablen im Falle eines Schleifenabbruchs wegen prim = false den kleinsten echten Teiler enthält, geben wir der Variablen den Namen teiler.
 

Lade  das Programm prim und speichere eine Kopie davon unter dem Namen prim1 ab. Versuche nun selbstständig das Programm mit Hilfe einer LOOP-Schleife zu formulieren. Unterstützung dazu findest du im rechten Teil dieser Tabelle. Mit dem Befehl iPart können die Nachkommsatellen einer Dezimalzahl abgeschnitten werden, d.h., iPart(4,23) = 4.

prim () Prgm Local prim, n, teiler ClrIO Request "natürliche Zahl (>1): ", n expr(n) ® n prim auf true setzen true ® prim 2 ® teiler  für die Ausgabe des Teilers teste, ob n gerade und ¹ 2 ist If mod(n, 2) = 0 and n ¹ 2   false ® prim Test für alle ungeraden Zahlen If prim Then   3 ® teiler   Loop   If mod(n, teiler) = 0   false ® prim       Exit     EndIf     If teiler > iPart(Ö(n))       Exit     teiler + 2 ® teiler   EndLoop EndIf Ausgabe in Abhängigkeit von prim If prim   Disp string(n)&" ist eine Primzahl" If not prim   Disp string(n)&" ist keine Primzahl ", Teiler: "&string(teiler) EndPrgm

Loop-Schleifen kommen vor allem dann zum Einsatz, wenn die Anzahl der notwendigen Schleifendurchläufe nicht von vornherein feststeht, wie im folgenden Beispiel.
 
 

Beispiel 10 ("Wurzelberechnungen") Bereits die Babylonier haben zur Berechnung der Quadratwurzel aus der Zahl n folgendes rekursives Näherungsverfahren verwendet:  Verwende dieses Verfahren, um Quadratwurzeln auf 10 Stellen genau zu berechnen.

 

Erzeuge die Programmvariable wurzel. Erzeuge folgende lokale Variablen: r (= Radikand), w (= Wurzel) und hlp (= Hilfsvariable, die xalt enthält). Lies den Radikand mit dem Befehl Request ein. Vergleiche deine Eingabe mit der Abbildung rechts.

wurzel () Prgm Local r, w, hlp ClrIO Request "Radikand", r expr(r) ® r EndPrgm

Um den TI-92 zu einer vernünftigen Anzeige des Ergebnisses zu bewegen, muss der Modus "Exact/Approx" auf "APPROXIMATE" eingestellt werden. Dies geschieht mit Hilfe des Befehls

setMode("Exact/Approx","APPROXIMATE").

Will man nach der Programmausführung die alten Einstellungen wieder herstellen, müssen diese am Programmanfang mit dem Befehl

getMode("ALL") ® Var

in der Variablen Var gespeichert werden. Die alten Einstellungen lassen sich am Programmende mit dem Befehl

setMode(Var)

wieder herstellen.
 
 

Auch alle anderen Einstellungen können mit diesen Befehlen geändert werden. Eine genaue Beschreibung der Befehle findest du  im Anhang A des Handbuches.

 

Füge die rechts angeführten Programmzeilen in dein Programm ein.

wurzel () Prgm Local r, w, hlp, sm getMode("ALL") ® sm setMode("Exact/Approx","APPROXIMATE") ClrIO Request "Radikand", r expr(r) ® r setMode(sm) EndPrgm

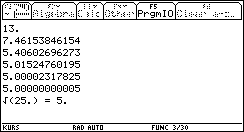
Je näher der Startwert (= das x_alt beim ersten Schleifendurchlauf) bei dem tatsächlichen Ergebnis liegt, desto schneller liefert das Programm das Ergebnis. Das Näherungsverfahren führt jedoch auch bei einem sehr schlecht gewählten Startwert, z.B.: x_alt=  r, verblüffend rasch zum gewünschten Ergebnis:
 
 

Füge die rechts angeführten Programmzeilen in dein Programm ein. Der Befehl abs(w - hlp) < 1.E-10 berechnet den Absolutbetrag der Differenz von w und hlp und vergleicht diesen mit der gewünschten Genauigkeit von 10-10.	... expr(r) ® r r ® w  Startwertfestlegen Loop   w ® hlp  xneu auf xalt speichern   (hlp + r / hlp) / 2 ® w   If abs(w - hlp) < 1.E-10     Exit EndLoop Disp "Ö("&string(r)&") = "&string(w) setMode(sm) EndPrgm
Starte und teste das Programm. Willst du auch noch beobachten, wie schnell die gewünschte Näherung erreicht wird, füge nach dem Befehl Exit noch die Befehle Disp w und Pause ein. Für r = 25 sollte dein Bildschirm dann wie die Abbildung rechts aussehen. Du musst nach jeder Ausgabezeile die -Taste betätigen, da der Befehl Pause das Programm solange anhält, bis die -Taste gedrückt wird.

Übungsaufgaben

 

Berechne mit Hilfe des Euklidischen Algorithmus den größten gemeinsamen Teiler zweier Zahlen. [Hilfestellung; Lösungsvorschlag] 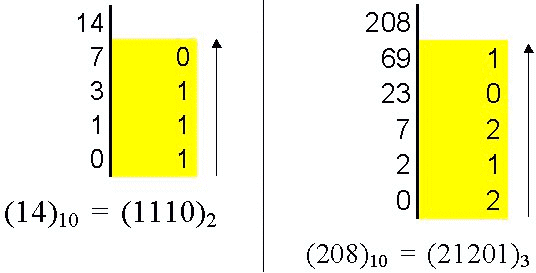Nachdem der Benutzer eine natürliche Zahl n eingegeben hat, soll das Programm diese Zahl in eine Dualzahl verwandeln und ausgeben. Die folgende Abbildung zeigt zwei Beispiele für einen Algorithmus, der dieses leistet: Dabei wird die eingegebene Zahl so lange ganzzahlig durch 2 dividiert, bis der Quotient Null ist. Die dabei auftretenden Reste (gelb unterlegt) ergeben von unten nach oben gelesen die gewünschte Dualzahl. Für die Zusammensetzung der Dualzahl ist dabei zu beachten, dass die Dualzahl nur als Zeichenkette dargestellt werden kann, da es keinen Datentyp "Dualzahl" gibt; d.h. der berechnete Rest muss für die Zusammensetzung der Dualzahl zunächst in einen String konvertiert werden. Bezeichnet rest den vom Programm errechneten Rest und dual die zu erstellende Dualzahl, so erreicht man dies durch den Befehl: string(rest)&dual ® dual. Weiters muss die Variable dual vor ihrer ersten Verwendung initalisiert werden; d.h. man speichert auf ihr durch folgenden Befehl einen Leerstring: "" ® dual. [Lösungsvorschlag]

Verschachtelte Schleifen

Lade  das Programm wurzel und speichere eine Kopie davon unter dem Namen wurzel1 ab. Ergänze dein Programm, wie rechts beschrieben. Die Funktion getKey() gibt den Tastencode der gedrückten Taste zurück. Wurde keine Taste gedrückt, gibt sie den Wert 0 zurück. Die Schleife am Ende des Programms wird also so lange wiederholt, bis der Benutzer eine Taste drückt. Hat der Benutzer die -Taste gedrückt, enthält die Variable taste den Wert 264 wodurch die äußere, rote Schleife und somit das Programm verlassen wird. Eine Übersicht der Tastatur-Codes findest du im Anhang B des Handbuchs.

wurzel () Prgm Local r, w, hlp, taste ... Loop ClrIO ... Disp "nochmal ... bel. Taste; Ende = ESC" Loop   getKey() ® taste   If Taste ¹ 0  Then     Exit   EndIf EndLoop If Taste = 264 Then   Exit EndIf EndLoop setMode(sm) EndPrgm