Stammfunktion
Eine Funktion F(x) heißt Stammfunktion oder unbestimmtes Integral von f(x), wenn
F'(x) = f(x).
Für das unbestimmte Integral verwendet man folgende
Schreibweise:
F(x) = 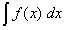
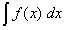
Das Integrieren ist die Umkehroperation zum Differenzieren: man sucht eine Stammfunktion F(x), deren Ableitung F'(x) = f(x) ist.
-
Im rechten Fenster siehst du die f(x) = x2-1 und ihre Stammfunktion F(x) = x3/3 - x.
-
Die Funktion f(x) hat unendlich viele Stammfunktionen der
Form G(x) = F(x) + c, wobei c
eine reelle Zahl ist.
Blende G(x) im GeoGebra-Fenster rechts ein und ziehe den grünen Punt entlang der y-Achse, um c zu verändern.
 Zeige mittels Differenzieren,
dass die folgenden Funktionen wirklich Stammfunktionen von
f(x)= x2-1
sind:
Zeige mittels Differenzieren,
dass die folgenden Funktionen wirklich Stammfunktionen von
f(x)= x2-1
sind:
a) F(x) = x3/3 - x
b) G(x) = x3/3 - x + 5
c) H(x) = x3/3 - x - 2.5
Stammfunktion und bestimmtes Integral
Jede Stammfunktion ist übrigens eine Flächeninhaltsfunktion von f(x). Warum das so ist, erfährst du beim Hauptsatz der Differential- und Integralrechnung. Kennt man also eine Stammfunktion F(x) von f(x), dann kann man das bestimmte Integral mit Hilfe dieser Stammfunktion berechnen: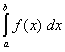 = F(b) - F(a)
= F(b) - F(a)