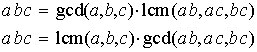A Plea for Pure Mathematics
I
am a teacher at a business college (high school level, 14-19 years) and
I have been working with CAS in teaching mathematics for a long time.
For many reasons I prefer DERIVE and I have prepared a lot of papers for
various purposes. In one of them we repeated and extended our knowledge
about GCD and LCM.
Unfortunately
was not possible to have regular access to the computer lab, because many
other subjects are more bound to the PC than mathematics. I tried to overcome
that obstacle. In last fall we - two colleagues and I - convinced the
parents of more than 150 students to buy a TI-92 to have a more interesting
and state-of-the-art mathematics education. I was teaching two forms and
after a short introduction into the handling of the machine (numerical
calculations, factorizing and expanding) I tried to do some "mathematics"
with my students (aged 15/16, approximately 65% female).
I´ll present the worksheet and add some comments (all in Italics). It was interesting and fascinating to observe the students´ attitude towards that kind of mathematics and I did not find any real differencies in attitudes comparing more or less gifted students
Using
the ![]() -Menu
you can factorize almost any arbitrary large number into its prime factors.
So let´s try the pretty large number 844074000! (Set your device in Exact
Mode!)
-Menu
you can factorize almost any arbitrary large number into its prime factors.
So let´s try the pretty large number 844074000! (Set your device in Exact
Mode!)
factor(844074000)
= ................................................

| (1) | Using that tool you can easily find the GCD of 844074000, 4765246200 and 45585540000. (Repeat first how to find the GCD of two or more numbers). |
| 844074000 = .......................................... | |
| 4765246200 = ........................................ | |
| 45585540000 = ............................., hence GCD = ........................ = ......................... | |
| At that moment students should revise a wellknown algorithm with larger numbers and expressions than usual. That is possible now using a CAS. |
| If the number found should represent the GCD, then all the quotients of the given numbers and the "maybe - GCD" should not have any prime factors in common. Check that now: |
So take:
| 844074000 : cd = ....................................... = .................... (factorize !) | |
| 4765246200 : cd = ....................................... = .................... | |
| 45585540000 : cd = ....................................... = .................... |
| true ? (yes / no) ..................... |
If your answer is no then check your result !
| This is a chance for the teacher to present a very easy to follow indirect proof. Some lessons earlier we showed in a short introduction into logic that a ® b is equivalent to Ø b ® Ø a. |
We want to show: If gcd(a,b) = T then gcd(a/T, b/T) = 1
We show that gcd(a/T, b/T) ¹ 1 implies T is not the gcd of a and b
| a : T = qa = p*a | (1) | |
| b : T = qb = p*ß | (2) |
| So | a = T * p * a and b = T * p * ß which implies that T * p must be a "greater" common divisor than T. And that is obviously a contradiction to the fact that gcd(a,b) = T. |
Find and check in a similar way the GCDs of:
| (3) | |
| (4) | 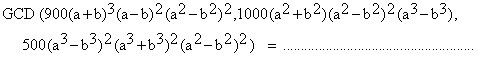 |
| (5) | 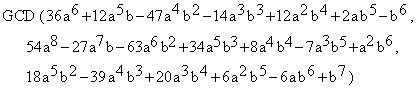 GCD = ......................................................................................... |
| These examples will force the students to check their data. They have to edit the bulky expressions very carefully. |
The TI-92 knows the function gcd(number1,number2) for calculating the GCD of number1 and number2.
Check that using two randomly chosen pairs of numbers:
| It was interesting to observe students trying to find a way out of that trap. At last they discovered the concept of a nested function. They immediately tried to extend for four or more numbers. |
| How could you use gcd for three or more numbers? | |
| = .......................................... |
| (7) | What is the meaning of the abbreviation gcd? |
| ................................................................................................... |
Have you ever tried gcd for non-integer numbers? Do that now and report your results:
| GCD(.....................................) = ...................................... | |
| GCD(......................................) = ...................................... | |
| GCD(......................................) =...................................... |
| Here we encourage the students to generalize a wellknown rule in an unusual way. They are asked to interpret the outcomes. |
I assume that you have tried only rational numbers, take now at least one irrational number:
| GCD(......................................) =...................................... |
(8) I also assume that you have worked with decimal numbers. It is "more mathematical" to work with fractions:
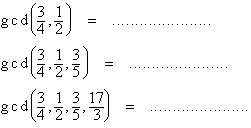 |
| Interpret the results: | |
| Does
your assertion hold also for |
|
| Is a new interpretation necessary? |
| Now we are learning that our first idea might not hold. We have to refine the interpretation. |
| (9) | The next task is to find the least common multiple for the numbers from (1): | |
| LCM (844074000, 4765246200, 45585540000) = .............................................. | ||
|
||
| (10) | Consider a check similar to that for the GCD! | |
| Describe the process: | ||
| Confirm your assumption using the numbers from (9) | ||
Find the LCMs for the expressions from (3), (4) and (5). Check the result for at least one of them:
| (14) is not interesting for English speaking students. But in Austria we call the lcm "kleinstes gemeinsames Vielfaches" with the abbreviation kgV. So this point forces them to use the manual and look carefully for the function wanted. |
| (14) | Which function of the TI-92 returns the LCM of two numbers: |
| ................................... | |
| (Use the manual!) | |
| (15) | What is the meaning of LCM for rational numbers? |
| (16) | I assure: |
| The LCM of two expressions a,b can easily be derived from the GCD(a,b) and the two expressions. Find the relation! |
Work systematically! Start your investigation using smaller numbers and try to find a rule.
| a = ....................; b = ....................., GCD(a,b) = ..................., LCM(a,b) = .............. | |
| a = ....................; b = ....................., GCD(a,b) = ..................., LCM(a,b) = .............. | |
| a = ....................; b = ....................., GCD(a,b) = ..................., LCM(a,b) = .............. | |
| a = ....................; b = ....................., GCD(a,b) = ..................., LCM(a,b) = .............. |
|
There are
so many patterns in mathematics and from my point of view recognizing
patterns can very often help students solve their maths problems.
So give them many chances to train that ability. |
GCD(a,b) =
Express this formula
in words:
Until now that conjecture has only been an unproved conjecture and not a theorem. The proof is still lacking. Try to follow carefully the exact proof:
a = 8400, b = 1440
a = 24*3*52*7 and b = 25*32*5 (*70)
gcd(8400, 1440) = 24*31*51*70 and lcm(8400, 1440) = 25*32*52*71
gcd * lcm = 24+5 * 31+2 * 51+2 * 70+1 = a*b
Let us generalize:
a = p1x1 * p2x2 *............* pnxn and b = p1y1 * p2y2 *............* pnyn
(with n = greatest prime factor occuring and if pk does not occur in one factorization then xk or yk = 0).
| gcd(a,b) = p1min(x1, y1) * p2min(x2, y2) * .................. | |
| lcm(a,b) = p1max(x1, y1) * p2max(x2, y2) * .................. | |
| hence |
gcd(a,b)*lcm(a,b) = p1min(x1, y1)+max(x1, y1) * p2min(x2, y2)+max(x2, y2) * .................. =
= p1x1+y1 * p2x2+y2 * .................. * pnxn+yn = a * b
|
This was
a welcome opportunity to present an exact proof in a mathematical
notation. It was helpful to refer at each step of the proof to the
example above, so the students could follow the process. |
| (17) | The above theorem might imply the consequence that we could generalize for three numbers / expressions: |
| a * b * c = lcm(a,b,c) * gcd(a,b,c) ?? | |
| Check the truth of that statement using two examples you choose yourself: | |
| (18) | Try the numbers 12, 30 and 64: |
| Are there any triples of numbers for which that formula holds??? | |
| (19) | Try for (12, 18, 25): |
| (20) | and now (150,210,330): |
| Can you explain the result? | |
| Sometimes you can have a "mathematical feeling" but it is not so easy to express that feeling in words. It is very important to train that ability. |
| (21) | Here is a real challenge: |
| Try to find a relation between GCD and LCM which holds in all cases: | |
|
The students found one solution:
At the time when I was busy with this paper in school I was running a T^3 seminar for Secondary School teachers and I presented this paper as an example for working with the TI-92. At 10 30 in the evening my phone rang and a colleague proudly told me that she had found a solution:
I wrote an e-mail to my friend Hannes Wiesenbauer and asked him for a - better? - solution. And he - as ever and whoelse - knew the answer. He wrote: "That problem is not so easy to solve, but there is a solution:" and he added a theorem which leads to
The two formulae show a wonderful symmetry and we could observe the principle of duality which the students had met a couple of weeks before when they had a short introduction into set theory and logic. You might imagine that it didn´t last very long and they asked if there was a dual formula for their product and fortunately there was. |
| (22) | The binomials of the form an ± bn with n Î N show special factorizations. Investigate these factorizations and summarize your results in an appropriate form (in words, in a table, formulas, rules, ......) |
| This was home work. I admit that this problem does not fit completely the gcd/lcm problems but it was a welcome opportunity for me to focus once again on pattern finding and last but not least the students had to compile their results in an appropriate form and present the results. |
| (23) | Unfortunately there is no function implemented in the TI-92 which allows to find the GCD and LCM of general expressions. So we will try to develop such a function. |
| Here are two functions ggt und kgv, which are working in a way presented on the TI-screen shown below. You should find the GCD and LCM of the expressions | |
| 360a4 + 1440a3 b + 1440a2 b2 and 45a3 – 180a b2: | |

..............................................................,
it will be sufficient to find a function for one of them.
Do you know any application of GCD and/or LCM?
The TI-function
getdenom(fraction) gives back the denominator of a fraction.
Try that using the following fractions:
What are the denominators
of the fractions: ![]()
Use ![]() to find the respective function which returns the numerator of a fraction:
to find the respective function which returns the numerator of a fraction:
.............................................
Check it: ................................................................
getdenom will support our task to find the function kgv!
Are you ready? Do you have a formula, which returns the LCM of two expressions t1 and t2?
Then define your function in the following way:
| We learn to define a selfmade function (and later to use it). |
and check its validity by applying it to the two expressions on the TI-screen - is it correct?
Congratulations! But to make sure: just one more little test:
Doublecheck your function for two numbers: kgv(3,6) = ....................
Everything ok? Why not?? What has happened?? Find an explanation and improve the function.
| Students should learn not be satisfied with their results too early. It makes sense to check the validity of rules even for very trivial cases. |
Improved version:
define kgv(t1,t2) = .............................................................................................
| We can use one function to define a new one. |
which leads immediately to
define ggT(t1,t2) = .............................................................................................
| In most cases calculating with fractions is an underdeveloped basic skill. Even in times of DERIVE and the TI-92 it is necessary to do simple calculations mentally or using paper and pencil. There are a lot of textbooks and collections of tasks together with the solutions. But it is not enough to have the problem followed by the solution. I say: "The way is the goal". So I tried to produce a paper to encourage students to train their fraction-handling-skills - if necessary - with the TI. And for that purpose they could use their selfmade kgv-function and doublecheck their calculations step by step.. |
| We have predefined a function ew(expr) which returns the expanding factor for a fraction with denominator expr and the given common denominator gn |
| Example 2:
|
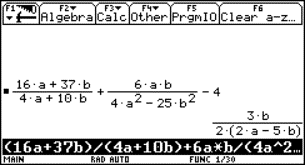
Can you find a reason why this calculation could cause a very special mistake?

Explain the last part in the edit line:
-4 * gn:
ew( )?
-4 * ew(....).
The remaining work is very easy:
Explain the relation between left and right hand side in the last row of the history area:

I want to close with a short summary. I like applied mathematics but I am sure that we can not do without pure mathematics. I found that the students liked investigating the problems presented and I spent a lot of time during the breaks to answer their questions (what if?, why not?, am I right?, do you think?,....). I never heard the question: What is the use of all that stuff? And I am teacher at a vocational school!!! So I think we can tempt pupils to have their "Adventures in Their Heads". And it is necessary to explain sometimes what they have done, like: "Now you found an important rule by your own!", "This is your first selfmade function!",... The students are really proud and their selfconfidence is growing. There were some very emotional moments when I felt that the sparkles were spreading and when I then left the classroom I felt something like: "that is it, I´ve got them". This are the precious moments when we learn why we have become teachers. I know that the use of a CAS in whatever form is not a necessary condition, but it is helpful in providing a new motivation for students and ............ not to forget, for teachers, too. One example of this species is just now standing in front of you.
What I have shown here using the TI-92 is platform - independent. I am sure that many chapters of our traditional curriculums can be changed and that it is not necessary to add many new topics as a consequence of the use of modern technologies. On the contrary, I must say, that I would now need more time in the classroom than before, because for me mathematics teaching has a much wider scope than ever before. And that without new subject matter.
Let me repeat in some keyterms what we have done besides revising the chapter CLM and GCD from Lower Secondary School (in order of appearence):
Indirect Proof
Exactness in Editing the Data
Concept of Nested Functions
Generalization 1
Interpretation and Reinterpretation
Reasoning, Defining, Checking
Using the Manual
Pattern Recognizing 1
Defining and Verbalising
Proof
Generalization 2
Try and Error, Exploring
Principle of Duality
Giving Reasons
Pattern Recognizing 2
Compiling the Results in an Appropriate Form
Defining Functions
Using Functions for other Functions
Checking functions even for trivial cases
Improving functions
Working with the functions