Basic Skills and Technology

 - not a Contradiction, but a Completion

   
by Josef Böhm
Bundeshandelsakademie St. Pölten
T3 - Austria and DERIVE User Group
   
   
Abstract  
 
  Are certain basic - manipulating and other - skills still necessary in math teaching? If so, then we should talk about which ones and in which amount. Some examples shall demonstrate that we can use modern computer and hand held technologies to encourage pupils and students of all levels to practise those skills which might be neglected in many cases using technology in math education. The examples presented have proved to be successful in classes but certainly there are many possibilities to improve the basic ideas in many ways using the features of all resources available at the moment.  
 

At almost all discussions on the use of CAS in teaching mathematics the question appears  mathematical basic (manipulating) skills are lost by using computers or not. At the same occasions it is emphasized by the members of the discussion that there is a need in investigating which basic skills are still necessary and in which amount.

I start from my point of view that - at this moment - we cannot and should not do without certain basic skills in mathematics. I feel unable to give any forecast for the future. I am sure that we could significantly rise the acceptance of technology in teaching mathematics by sceptic and critical teachers or technology refusing educational systems if we would be able to apply technology not only to present real life problems or new - for some people radical - didactical approaches but also to improve basic calculating and manipulating techniques and mathematical capabilities. We can very consciously practise all those techniques using technology which could be neglected by a (too?) intensive use of the technology.

It would be necessary and helpful to set up a list of such basic skills which teachers would like to have practised by their students. From my own experience I can say that it is very useful to provide tools for the pupils - or students which enable them to help themselves in case of troubles and difficulties. It is not sufficient to have a textbook with lots of examples followed by the solutions and the students don´t find the way from the problem to the solution. At the other hand it is not sufficient to have problems followed by a step by step solution. Sometimes it could be useful to work out a student - computer interactive strategy to help overcoming some deficiencies.

I collected some skills which could be practised and improved using computers (that is only a glimpse and I know that the discussion could lead to the conclusion: "we don´t need this or that  any longer in computer age".).
 
  • Estimating numerical results
  • Working with percentages
  • Working with fractions
  • Applying elementary algebraic operations (factorising, ......)
  • Recognising types of functions by their graphs
  • Using functions (Relations)  and their various representations
  • Solving equations (linear, quadratics and systems of equations)
  • Calculus techniques
  • Improving 2D and 3D imagination
  • Calculating mentally
  • Transformations of function
 

Incited by ideas from Jan Vermeylen (Belgium), Heinz Rainer Geyer (Germany) and Johann Wiesenbauer (Austria) I tried to produce training- and practise programs for my students (secondary level II), which I want to present as seed for further developments. The platforms are DERIVE and the hand held revolution, TI-92/89. The only reason for this choi ce is because I mainly use those to CAS. I am sure that you can use each of the available systems. The goal should remain the same: developing softeware products which will meet our - the teachers´ and the students´- very special wishes, ideas and visions.

I have tried to work with such tools since long. In my first years working with computers I produced programs written in BASIC. It is quite nice to follow the development of hard- and software on one application: The Rule of Vieta, presenting random generated examples.

I will allow a nostalgic look into the program code – I am happy to have done this a couple of years ago. It helps a lot to write programs with modern software tools.
   
   
   
Then I changed to DERIVE working with a class in the computer lab:
   
The idea remained the same, the tool changed and it changed once more to hand held technology.
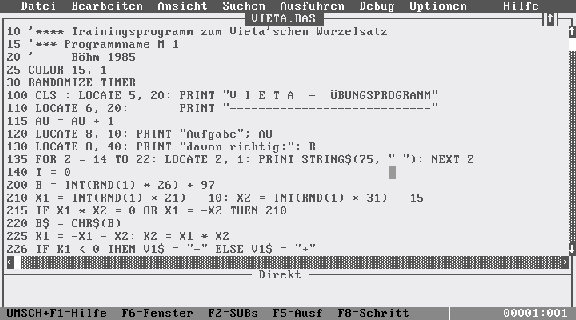
I rediscovered my old BASIC-program, converted it to the TI´s syntax and my students practised
"Vieta" in the lessons, in the breaks, at home, sometimes in the train or sometimes just for fun or – how a girl told us – as a means to find her concentration before learning for other subjects.
   
Practise the Rule of Vieta!  
   
   
Allow me another memory of my BASIC past: a program to revise the students´ knowledge on set theory. I am still using this tool, the students like it and it doesn´t take too long time to achieve quite reasonable results.
   
   
Some other examples are following:  
   
Practise factorising (Jan Vermeylen)  
   
   

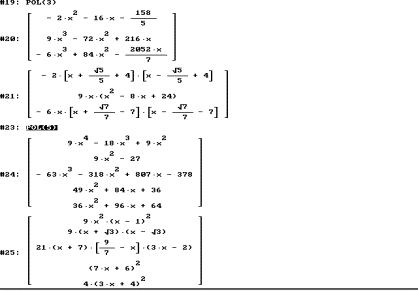
POL(n) produces n random number generated problems.

The students have to factorise using pencil and paper and then check their solution.

The file could easily be changed to practise special types of factorizations if necessary.

Settings of factorization modes - Rational, Complex, ... – gives a nice variety of points of view.
   

(This example is some years old and could be adapted to other platforms)

Then it could look like the next trainings tool (JosefBöhm). My students like it and use it:
   
I will demonstrate the program including error analysis and Help function. We want to practise cubics of binomials 

   
   
   
   
The screen shots are self explanatory.  
   
They practised squaring and cubing binomials, squaring trinomials, multiplying binomials mentally and with "The Quiz" they were presented a random generated sequence of problems. So you can have competitions in the class room and the pupils become very,very busy, even the weaker ones.
   
The next example is from H.R.Geyer to help students improving their mentally calculation skills.
   
   
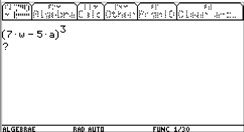
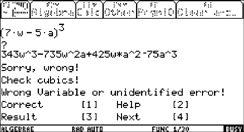
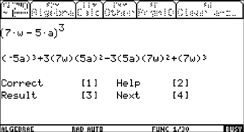
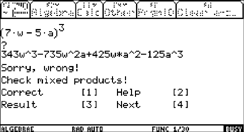
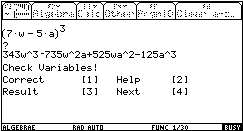
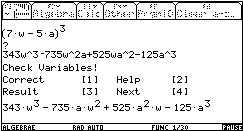
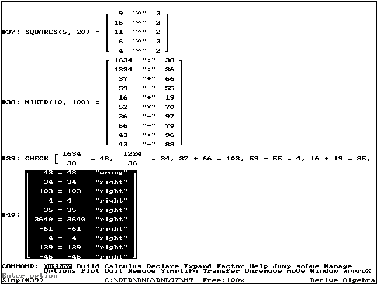
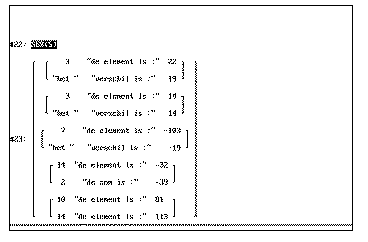
Textfeld:
J. Vermeylen produced a DERIVE file to have lots of "standard problems" dealing with arithmetic series. "verschil" is Dutch, it is the difference d of the series.
   

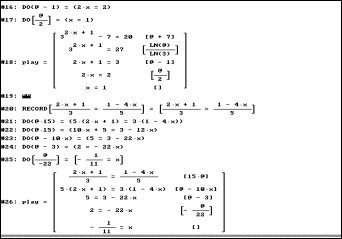
The next screen shot is the final result of a very busy discussion in the DERIVE community to produce a sort of report when solving an equation and applying various equivalence transformations.
Johann Wiesenbauer - who else - solved the problem with a very sophisticated tool.

So students are able to reproduce, what they have done using paper and pencil and check their results with the computer´s ones. They find their mistakes by themselves.
   
   
I found it useful and necessary as well that students can find the equation of a linear function, seeing its graph. They also should be able to have an imagination of the graph seeing the linear function very quick: "Match the Line!". Then I added some other tasks, as finding parallel and perpendicular lines by inspecting the grid and applying the various forms of the equation for a line
   
   

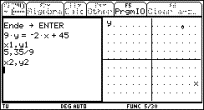
Another course of the Lines-Menu: "Find two points!"

You enter the coordinates of two points which should ly on the given line, see two "balls" on the grid and if you are lucky the line passes the two "balls". The linear function appears in various representations (explicit, implicit, ..)
   
Finally I produced a "game". Give some random points on the grid and let the students hit them with as few lines as possible, or do that with parabolas ......
   
   
Another tool helps my calculus classes to improve their calculus techniques. I transmit the program calc() on their TI-92/89s and then they are able to practise whenever they have some time and what they believe to be necessary for them:
 


 
   
I know that there can be lots of improvements. It would be better to explain the way how to do it correctly to have really a learning tool. What do you say to the next program, written by Philippe Fortin from France. He calls his program "stepder" from "Stepwise deriving functions":
   
   
   
   
The last example is part of a whole sequence to teach the pupils how they can help themselves reaching a sound level in working and manipulating with fractions.
   
Before working with fractions we had together developed a function kgv to calculate the LCM of two general expressions, to check the common denominator and then we used a selfmade function ew(expr) to find the expanding factor for the denominator expr with a common denominator gn.
   
Step by step the students can perform their calculation and check it using the calculator.
   
   
From the TI 92 Worksheet 3  
   
We have predefined a function ew(expr) which returns the expanding factor for a fraction with denominator expr and the given common denominator gn
   
Train your skills in calculating and manipulating with fractions
   

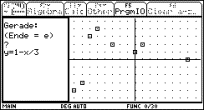
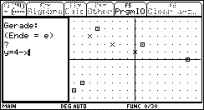
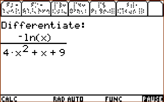
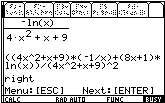
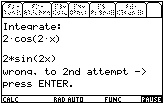
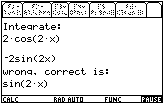
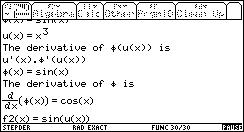
Example 2: 
   
Calculate without the TI. Write down your result  
   
Here it is.  
   
Can you find a reason why this calculation could cause a very special mistake?
   
Compare the common denominator and the factors used to bring all the numerators over a common denominator.

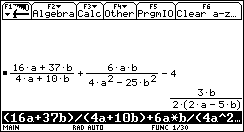
Explain the last part in the edit line:

  -4 * gn:

How to work with an expanding factor
ew( )?                               -4 * ew(....).
   
The remaining work is very easy:

Explain the relation between left and right hand side in the last row of the history area:
   
The underlying basic idea sounds very strange and controversary:
   

In addition to all the wellknown reasons to include modern technologies into mathematics teaching, which I like and support in a very high degree, I also use the technology in many cases to improve manipulatings skills which seem to be no longer of any importance by using these technologies.

If you would like to try some of the tools presented in this paper, then please contact me. I would appreciate any suggestions and ideas dealing with this topic. The TI-92/89 programs algebra(), lines() and calc() are distributed together with the bk teachware books (references).

Very recently I turned back again to my "first love" DERIVE - with version 5. Fortunately my colleague Tania Koller and I could split a class for mathematics and we are working with DERIVE in the PC-Lab. Using the programming capabilities of DfW5 I tried to transfer my DERIVE for DOS - TI-92 - ideas back on the PC-screen. And it worked wonderful:

Although the screen shot is in German, but I think that you can follow:
   
   
   

qu= presents a square a random generated square, ku= a cube, tr= a square of a trinomial, pr= a product of two binomials of form (a var1 + b var2) (c var1 + d var2) and the student is asked to perform the multiplication mentally, di= gives a product of form (a var1 + b var2) (a var1 - b var2) and finally te= brings a randomly chosen task on the screen. qub(n)= presents n problems of form qu, etc.

You can see that the learning and practising tool will not only provide the correct result with res=, but and that is important gives an advice where to look for the mistake.
   
The underlying programming structure can be found in [9].
   
I used a similar idea to practise factorising general expressions and/or polynomials
   
   
DERIVE "offers" the task and the student who should perform the manipulation using paper and pencil and then check his/her answer. See one example for factoring out ("Herausheben") and a sequence of three problems to apply factoring out together with factoring a difference of squares.
   
   
The acceptance and the enthusiasmus of the students were the best confirmation for my work.
   
One can factorize polynomials on different levels of mathematical knowledge:

ch= gives rational linear factors only,

chw= returns also the irrational way and if

appropriate

chk= shows the complex factorization.
   

References:

[1]   Geyer, H. R ,Vermeylen, J.,Wiesenbauer, J., Welke St. (1998). From Nested Ifs to a MACRO for
DERIVE. DERIVE & TI-92 Newsletter #31
[2]   Vermeylen, J. and Böhm J. (1995). Vieta by Chance. DERIVE & TI-92 Newsletter #20
[3]   Geyer, H. R. (1997). The "Delayed” Assignment :==. DERIVE & TI-92 Newsletter #27
[4]   Böhm, J. (1998). Train your skills with the TI-92. DERIVE & TI-92 Newsletter #31
[5]   Böhm J. (2000). Mathe Trainer I. bk teachware, Hagenberg, Austria
[6]   Böhm J. (2001). Maths Trainer I. bk teachware, Hagenberg, Austria (to appear)
[7]   Fortin, Ph. (1999). Introduction au Calcul Formel. T3 Europe - France
[8]   Böhm J. (2000). DERIVE & TI-92 Newsletter #40