Give it a Spin!
BHAK St.Pölten, T3 and DUG, Austria
One of the MFAQ (= Most Frequent Asked Questions) after workshops or lectures on the usage of modern technologies like the TI-family, DERIVE, MS-EXCEL or others for maths education in Secondary Schools is how to find problems and tasks for exercises and assessment. Many of the more experienced teachers have a collection of problems of their own and it is very understandable that they don´t want to throw all their treasures away and start again like at the very begin of their career as a teacher.
I was and still am in the same situation. My standard answer is: you don´t have to change everything, take your problem collection and try to achieve another point of view. Then in many cases you will be able to give the problems a spin into the right direction and thus they will adopt a new quality, focus on another aim as usual, open new insights or just let it read a bit uncommon.
Please don´t expect results of a deep scientific research on that topic within the next short hour and don´t expect any classification of how to give "special spins". I am an ordinary school teacher on a Secondary College for Business Administration in St.Pölten, the capital town of Lower Austria. I also have been busy in in- and pre-service courses for teachers and give a lecture on the use of modern technologies in maths education on the Vienna Technical University. So you can imagine that I am very deep involved in the discussion mentioned above.
On my school we teach mathematics for four years - age 16 - 19, and I decided to follow these four years and selected problems from my recently given written and oral examinations - unchanged for this presentation. I hope to give some insight into the daily work of a school teacher who has been using DERIVE and the TI since long. Most of the examples presented here are software independent. I choose the TI, because it prooved to be the easiest platform for presentations using the ViewScreen.
When we start using
the PC or hand held technologies in maths education we have to make the
students accustomed to the machines as quick as possible. I do the same
what I did years ago with ordinary pocket calculators: evaluate more complicated
numerical expressions and learn them to differ between decimal digits
and significant digits. But now the students not only note the results
but also learn to compare the given problem with its output on the screen.
|
|||
By the way the students do not only practise linearizing the expressions, but also get accustomed with fraction powers for roots and floating point notation.
Then we work with basics in algebra manipulations like working with fractions, binomials and polynomials, solving linear equations etc.
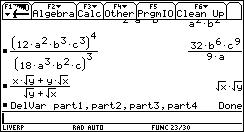
I don´t ask my pupils to evaluate a fractional monster like the next one by hands - although we sometimes do it in class room - in an assessment, but they shall be able to edit this expression applying various strategies:
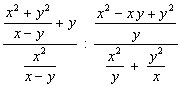

Given
are some elements of a binomial´s power. Complete and find the task: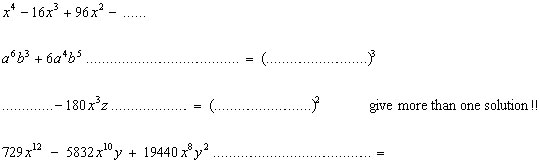 (in cooperation with my technology - co-fighter, Tania Koller from my school, the BHAK St.Pölten) |
We´ll change to linear equations. Combine testing manual calculation skills with responding on new questions.
|
|||||||||||||
Plenty of new - very mathematical, and not too easy to answer - questions are offered only by inspecting the CAS´ output. Let´s make more use of this new possibilities.
See also the next
example how to combine
- indespensible? - basics and computer algebra.
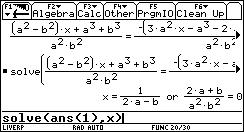
|
|||||||
I don´t know your experience, but in my teacher´s career not learning but applying the power rules is one of the major problems for the students.
It is no problem to use also the support of a CAS to train these basics:
See an example from a "Basics´ Test" given in my project class where we differed between basics- and problem solving tests.
|
|||||||||
| Translation: | A2) | Evaluate with the pocket calculator and give reasons for the result. |
| A3) | Give an explanation for the calculator´s output. |
Sometimes the calculator´s results are looking very
strange and so it is not necessary to forbid its use:
Collect the result and write it down without use of any denominator:
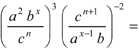
|
Use
the TI: Expand(ln(9000)) = |
|
Apply
the appropriate logarithmic rule to expand ln (b-4)5. |
Collect
the logarithms by hands, try to do your best with the TI and compare
the results, explain the different forms of the results.
|
|||
We should take the chance and force our students to enhance graphical and numerical methods and make these two methods partners of analytical methods with equal rights.
|
|||
| Solve
the simultaneous equations for x and y: Find at least two pairs (a,b), which make the system non soluble! |
A female student put the variables into the correct order and immediately noted (-3,2) and (1,1) as answer for the second question. I was surprised and asked her how she had got the answers.
She explained:
|
Equations
containing trig functions are called "goniometric equations":
Solving such equations needs a lot of tricks and can become very
tiresome. Using the TI you can try to solve equations of this kind
on various manners. How many solutions are there? Can you express a general solution in mathematical terms? (or in words?) |
Plot
the graph of
|
|||||
Find
a 4th degree polynomial function with
Plot their graphs. Can you set up any conjecture? If so, then use two other polynomials of other degrees to confirm your conjecture. |
|||||||
|
|||
So I was very curious about the "success", and it worked. Surprisingly the weakest pupil was the first one to have the "correct" solution. Why "correct" under quotes? Look carefully! During the test one pupil raised her hand: "Sir, I think that there is something wrong! I am sure that this problem deals with a cone, but in the edit line under the root must be the expression for the cone´s height, given by the sideline 12 and the radius. The application of Pythagoras´ Theorem seems to be wrong!".
And indeed, as I mentioned before, I set up the test in the late evening and I made a mistake. Three out of 18 pupils found this mistake ................... and earnt an extra credit.
MariaLuise Müller, a colleague from another school - BHAK Waidhofen/Ybbs
- saw this example at any occasion and tried to transfer the idea to a
financial mathematics problem.
The task sounded very clear:
Tell the story of this business!
| Five
spheres (R = 3.17 inch) made of brass are melted down and a cylinder
with r = 6,34 inch is casted. What is the cylinder´s length? |
|
Five points ABCDE form a pentagon: AB
= 264, BD = 996, AD = 1128, DC = 444, What is the length of segment EC? What is the pentagon´s area? |
|
|||||||||||||
|
|||
Obviously this can be extended for investigating boundaries and limits.
CAS and graphing calculators and programs like DERIVE opened a wide field to "investigate" functions not only in the traditional way (zeros, extremal values and inflection points ....)
| a) | Produce a sketch of the graph |
| b) | Investigate the discontinuities. |
| c) | Are there other "interesting" places? |
| d) | Define y(x) as a piecewise defined function and check your definition by superimposing the graphs. |
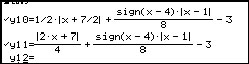

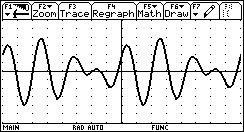
I have best experiences with "descriptions of pictures" with the pictures being graphs of sometimes a bit exotic and strange functions. The students appreciated this work. I have a table full with 60 such functions and each of the students has 5 randomly chosen functions to "describe" including a nice sketch of the graph and a summary of its special points, discontinuities, behaviours etc. In most cases it is not sufficient to only copy the graph from the screen, because eg. very often poles and jumps do not appear as poles and jumps. The screen´s resolution produces wrong connections of points and makes necessary an accurate investigation of limits. Scaling has to be adjusted etc.
13.
14.
15.
35.
36.
37.
32.
38.
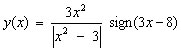
Use
CAS to investigate the discontinuities. |
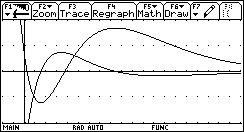
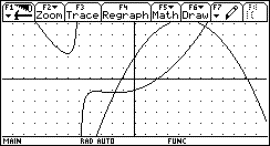
Decide: which of the graphs is the function and which one is the derivative? Give reasons for your decision.
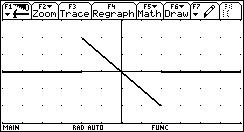
You see the graph of function y(x). Add the graph of its continuous antiderivative, passing P(-3,-2).
|
An - in pre TI-times - important calculus application in school mathematics were the so called "Curve Discussions". The students had to calculate (by solving a lot of equations)
|
|||||||||||||||||||
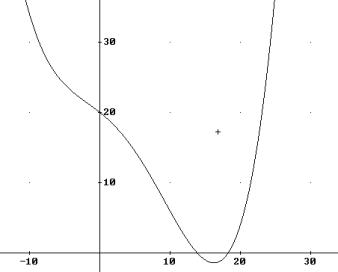
Or the other way round: find the function term of a 4th degree polynomial, knowing an inflection point at ...... You know all these problems, leading to a system of linear equations.
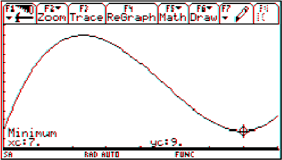
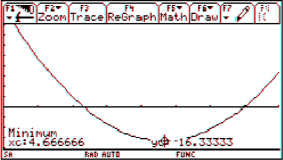
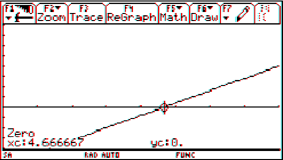
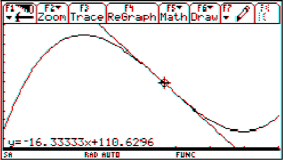
I prefer presenting a graph and giving the task to find an approximating function. The students have to figure out suitable data, read off the numbers and compare their results with the given graph. Calculating is no problem any longer. (I´d like to remind many of you on Paul Drijvers´ ghost!)
I think it would be even better to present a hand sketch. Many variations
are possible:
have different scales on x- and y-axis, ask to use only two or three points to force the students to consider the slope or any other attribute, too. Make it not too easy reading off the coordinates of sufficient points. Add poles and/or horizontal asymptotes. I can assure you that the students appreciate this type of problems. But I also must admit that grading the tests has become more difficult and time consuming as ever before.
This is the function of the graph presented above:
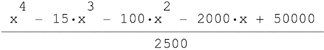
Eleonore Eisler,
a colleague from Tulln, Lower Austria and member of our project group
in investigating possible changes in assessment using technologies in
maths teaching gave the following task in the frame of a "problem
solving test" (following ideas from Hildegard Urban-Woldron, Lower
Austria):
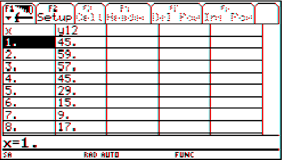
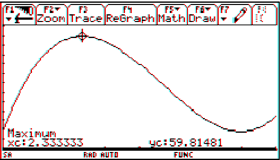
|
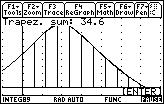
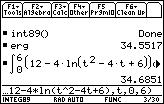
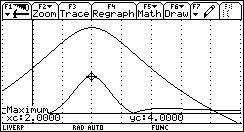
The concentration M [grams/liter] of a 6-hour allergy medicine in a body is modeled by
where t is the time in hours since the allergy medication was taken. Find the average level of concentration in the body over the 6-hour period.
|
|||||||||||||||||
Idea from (Calculus, Larson & Edwards, Houghton Mifflin 1999, ISBN 0-395-91683-6) [3]
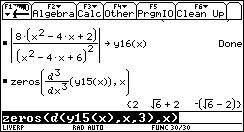
- Include the graphing capabilities for additional tasks - forcing visualization.
- Encourage and ask for numerical and graphical solutions, ask for more than one way of solution, accept heuristic methods, encourage and ask for "Try and Error Methods".
- Let the pupils produce self made tools and give opportunities to apply them.
- Provoke functional thinking.
- Find the problem to presented solutions.
- Let the pupils set up conjectures - but also ask sometimes for the proofs.
- Include the various ways of the CAS´ output into the task, interpret the output and compare with calculation by hands, make the CAS built-in simplification rules to a mathematical subject.
- Use the CAS-capabilities for additional questions (and keep staying within the curriculum!!)
- But over all take care that you don´t give problems which set the calculator in the center of the problem, we should remain guided by mathematics and not by the manual.
[1] Einführung
des Integralbegriffs mit dem TI-92, J Böhm & W Pröpper, bk-teachware
SR-13
[2] Exploring
Integration with the TI-89/92, J Böhm & W Pröpper, bk-teachware SL-12,
to appear in 2000
[3] Larson
& Edwards, Calculus, Houghton Mifflin 1999, ISBN 0-395-91683-6
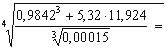 (2 significant digits)
(2 significant digits)