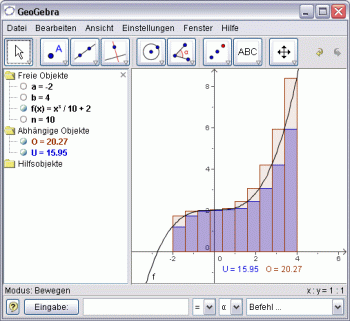
Unter- und Obersummen mit GeoGebra

Berechne für folgende Funktionen mit Hilfe von GeoGebra die Fläche zwischen x-Achse und Funktionsgraph im angegebenen Intervall näherungsweise mit Unter- und Obersummen. Eine kurze Anleitung, wie das mit GeoGebra geht, findest du weiter unten auf dieser Seite. a) Fläche unter 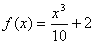im Intervall [-2, 4] b) Fläche unter 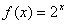im Intervall [0, 2] c) Fläche unter 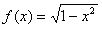im Intervall [-1, 0]. Wie groß ist die Fläche des gesamten Kreises? Hinweis: sqrt(x) ist die Wurzelfunktion in GeoGebra Start GeoGebra Dein Ergebnis sollte mindestens auf die Einerstelle genau sein. Schreib deine Ergebnisse zusammen mit der Anzahl der verwendeten Rechtecke in dein Heft.

Kurzanleitung zu GeoGebra

Wenn du GeoGebra noch nicht gut kennst, hilft dir die folgende Anleitung bei dieser Übung:

1. Starte GeoGebra, indem du oben auf die Schaltfläche "Öffne GeoGebra" klickst.
   
2. Gib in die Eingabezeile eine Funktion ein, z.B. f(x) = x^2, und drücke die Eingabetaste.
3. Gib die Intervallgrenzen a, b und die Anzahl der Rechtecke n ein (drücke jeweils die Eingabetaste):
   a = -1
   b = 3
   n = 5
4. Lass GeoGebra die Unter- und die Obersumme berechnen:
   U = Untersumme[ f, a, b, n ]
   O = Obersumme[ f, a, b, n ]
5. Wähle den Bewegen Modus in der Symbolleiste und klicke im Algebrafenster auf die Zahl n. Mit den Pfeiltasten der Tastatur kannst du jetzt n verändern. Wenn du auf n doppelklickst, kannst du der Zahl auch direkt einen neuen Wert geben (Eingabetaste nicht vergessen). Auf diese Weise kannst du auch a und b verändern.
   Tipp: klicke mit der rechten Maustaste auf n, wähle "Eigenschaften" und setze dort die Schrittweite auf 1. Dadurch bekommst du bei Veränderung mit den Pfeiltasten nur natürliche Zahlen für n.
6. Um eine neue Funktion zu untersuchen, gibst du diese einfach in die Eingabezeile ein, z.B. f(x) = sin(x) + 1, und drückst die Eingabetaste.