Übung: Stammfunktionen händisch bestimmen

Das Integrieren ist die Umkehroperation zum Differenzieren:
Man sucht eine Stammfunktion F(x) = _∫f(x) dx, deren Ableitung F'(x) = f(x) ist.
Aus den Differentiationsregeln erhält man sofort einige einfache Regeln zum Ermitteln von Stammfunktionen.
In der folgenden Übung wirst du versuchen, für verschiedene Funktionen f(x), jeweils eine Stammfunktion F(x) zu finden.


Musterbeispiel:

Wir wollen eine Stammfunktion der Funktion f(x) = x⁵ finden.

Wir überprüfen ob F(x) = x⁶  eine Stammfunktion von f(x) ist: F´(x) = 6 x⁵ ≠ f(x)
⇒ F(x) ist also keine Stammfunktion von f(x).

Man erkennt aber, dass die Funktion G(x) = 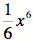 eine Stammfunktion von f(x) ist. Probe: G´(x) = x⁵ = f(x)

Auch die Funktion H(x) = 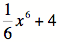ist eine Stammfunktion von f(x): Probe: H´(x) = x⁵ = f(x).
Daher ist auf der Seite Integrationsregeln immer die Integrationskonstante C angeführt.

Aufgaben:

Versuche für die folgenden Funktionen eine Stammfunktion zu finden und überprüfe diese durch Differenzieren!

a) f(x) = 4

b) f(x) = x3

c) f(x) = x½

d) f(x) = x -2

e) f(x) = sin (x)

f) f(x) = cos (2x)