Flächeninhaltsfunktion und bestimmtes Integral
Mit Hilfe einer
Flächeninhaltsfunktion A(x) zur gegebenen Funktion f können wir den
Wert des bestimmten Integrals im
Intervall
[a, b] sehr einfach berechnen:
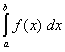 = A(b) - A(a)
- Im rechten Fenster
siehst
du eine Erklärung für diese Situation
dargestellt, wobei du mit den Pfeiltasten Schritte vor bzw. zurück
gehen kannst. Du kannst außerdem jederzeit die Intervallgrenzen a und b
verschieben.
Versuche in eigenen
Worten die obige Formel zu erklären. Mache auch eine Skizze in
deinem Heft.
 Berechne
mit Hilfe der
Flächeninhaltsfunktion bezogen auf die untere Grenze (-1),
nämlich
A(x)
= x3/3
+ 6x +
6.5,
die Fläche unter dem
Funktionsgraph von f(x)
= x2
+ 6 im Intervall
[0.5, 6] in deinem Heft! Berechne
mit Hilfe der
Flächeninhaltsfunktion bezogen auf die untere Grenze (-1),
nämlich
A(x)
= x3/3
+ 6x +
6.5,
die Fläche unter dem
Funktionsgraph von f(x)
= x2
+ 6 im Intervall
[0.5, 6] in deinem Heft!
Vergleiche dein Ergebnis mit der Konstruktion im rechten Fenster!
|
|
Ergebnis
Wir wissen jetzt, dass wir mit einer
Flächeninhaltsfunktion ganz einfach
das bestimmte Integral berechnen können.
Die Frage ist nun: Wie bekommt man so eine
Flächeninhaltsfunktion?
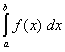 = A(b) - A(a)
= A(b) - A(a) Berechne
mit Hilfe der
Flächeninhaltsfunktion bezogen auf die untere Grenze (-1),
nämlich
Berechne
mit Hilfe der
Flächeninhaltsfunktion bezogen auf die untere Grenze (-1),
nämlich