Das bestimmte Integral

In den bisherigen Übungen hast du gesehen, dass für die Fläche A unter der Funktion f(x) immer gilt:

Untersumme U ≤ Fläche A ≤ Obersumme O

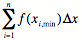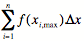
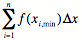≤ Fläche A ≤

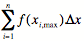
Bei wachsender Anzahl n der Rechtecke wird die Breite Δx jedes Rechtecks immer kleiner und Unter- und Obersumme nähern sich immer mehr einander an.

Daher definieren wir die Fläche A unter der Funktion f(x) im Intervall [a, b] als Grenzwert von Unter- und Obersumme:

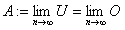Diese Fläche heißt bestimmtes Integral von f(x) im Intervall [a, b], das wir so schreiben:

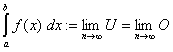
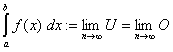
Das Integralzeichen ∫ stellt ein stilisiertes "S" dar und steht für "Summe". Das "dx" steht für die unendlich kleine Breite eines Rechtecks, wenn n gegen unendlich geht.

Diese Schreibweise soll verdeutlichen, dass es sich beim bestimmten Integral um den Grenzwert einer Summe von Produkten handelt.