Flächenberechnung
In dieser Übung berechnest du Flächen mit GeoGebra oder Maxima. Beide Programme bieten dir Befehle für das bestimmte Integral einer Funktion f(x) in einem bestimmten Intervall [a, b].| gewünschte Berechnung | Befehle | ||
| GeoGebra |
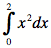 |
f(x) = x^2 Integral[f, 0, 2] |
|
| Maxima |
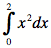 |
f(x) := x^2; integrate(f(x), x, 0, 2); |
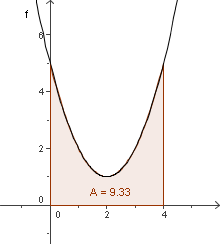
MusterbeispielWir berechnen die in der Abbildung rechts gekennzeichnete Fläche unter dem Funktionsgraphen von f(x) = x2 - 4x + 5 mit GeoGebra:
|
 |
Berechne
für die
folgenden Funktionen die farbig
gekennzeichneten Flächen mit GeoGebra oder Derive. |
a) 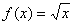 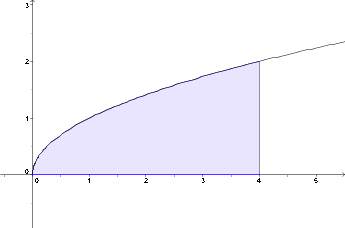 Lösung a): 5.33 |
b) f(x) = 3 - x2 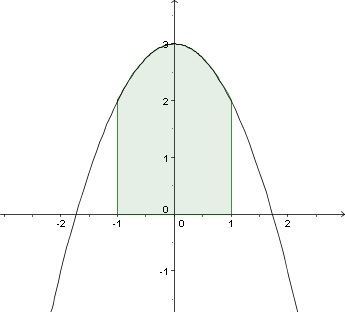 Lösung b): 5.33 |
c) f(x) = 0.5 x2 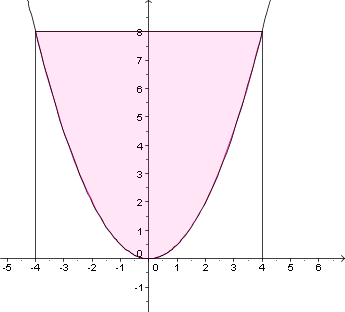 Lösung c): |
d) f(x) = (x - 5)2 - 4 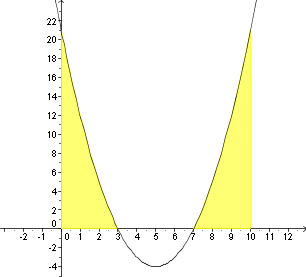 Lösung d): 54 |
e) f(x) = (x - 5)2 - 4 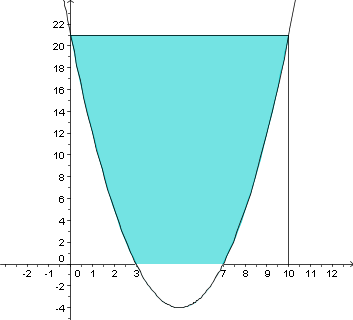 |
 Aufgaben
Aufgaben