Die Umkehrfunktion der Exponentialfunktion
Aufgabe: Konstruiere die Umkehrfunktion zur Exponentialfunktion f(x) = ax.
Gehe dabei folgendermaßen vor:
▪ spiegle den Punkt P an der 1.Mediane y = x (Spiegle Objekt an Geraden).
Der dadurch erzeugte Punkt heißt P'.
Zeige mit einem Rechtsklick seine Beschriftung an.
▪ Zeichne eine Strecke von P nach P'
ein.
▪ Zeichne den Graph der Umkehrfunktion als Ortslinie von P' (Befehl Ortslinie[P',P] )
Verändere die Basis a und bewege den Punkt P auf dem Graphen der Exponentialfunktion.
Beobachte das Verhalten der beiden Funktionsgraphen und beschreibe
in eigenen Worten, was dir auffällt (Definitionsmenge, Wertemenge,
Monotonie).
© Medienvielfalt und Mathematik-digital 2011, erstellt mit GeoGebra
| Lösung ausblenden |
In der obigen Lösung wird bei der Exponentialfunktion f(x) = ax für die Basis a = 1 auch die gespiegelte Gerade gezeichnet.
| Lösung ausblenden |
| Der Graph der Exponentialfunktion y = 1x = 1 geht durch Spiegelung in eine senkrechte Gerade über, die kein Graph einer Funktion ist. Bei einer Funktion muss jedem x-Wert stets eindeutig ein y-Wert zugeordnet werden, und dies ist hier nicht der Fall. |
Eine Funktion f: R+ → R, f(x) = alog x heißt Logarithmusfunktion zur Basis a (aÎR+\{1})
Zusammenhang zwischen Logarithmusfunktionen und
Exponentialfunktionen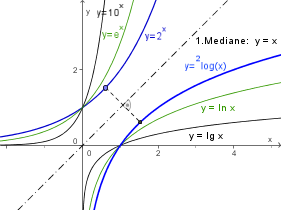
Der Graph einer Logarithmusfunktion geht durch Spiegeln an der 1.Mediane aus dem Graphen der entsprechenden Exponentialfunktion hervor.
Hinweis: In der Skizze bezeichnet lg x den Zehnerlogarithmus 10log(x) zur Basis 10 (logarithmus generalis).