Differentialquotient - Übung 2

Übung 2a

Hier wird die Steigung der Tangente an f(x) = x3 + 5 an der Stelle 1 berechnet, also der Differentialquotient f'(1) bestimmt. Vollziehe alle Schritte dieses Beispiels nach, indem du auf den rechten Pfeil klickst.

Laut Definition ist der Differentialquotient: ▼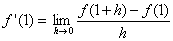
in f(x) einsetzen: ▼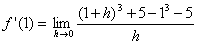
Klammer ausmultiplizieren: ▼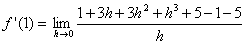
zusammenfassen: ▼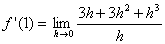
h herausheben: ▼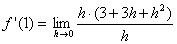
durch h kürzen: ▼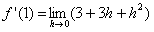
Grenzwertberechnung: ▼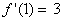
Lösung: Die Steigung der Tangente an f(x) = x3 + 5 an der Stelle 1 ist 3.

Übung 2b

Bestimme die Steigung der Tangente an f(x) = x3 + 5 an der Stelle 2 in deinem Heft.

Übung 2c

Bestimme die Steigung der Tangente an f(x) = x3 + 5 allgemein an der Stelle x0 in deinem Heft.

Übung 2d

  • Berechne die Steigung der Tangente an f(x) mit Hilfe des Ergebnisses von Übung 2c an mindestens drei Stellen in deinem Heft.

  • Überprüfe deine Ergebnisse, indem du im rechten Fenster die Stelle x0 mit der Maus einstellst.

  • Hast du in Übung 2b richtig gerechnet?
 

© M. Hohenwarter, 2005, erstellt mit GeoGebra