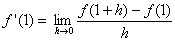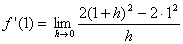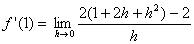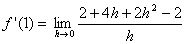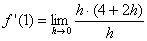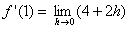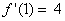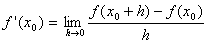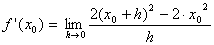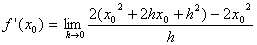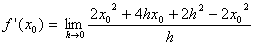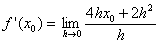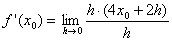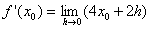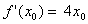Differentialquotient - Übung 1
Übung 1a
Wir wollen die
Steigung der Tangente an f(x)
= 2
x2
an
der Stelle x0 = 1 berechnen.
Das rechte Fenster zeigt diese Situation:
-
Mache den Wert von h immer kleiner,
indem du im rechten Fenster den roten Punkt nahe zu x0 = 1 ziehst.
Beobachte dabei die Steigung der Sekante (den Wert des
Differenzenquotienten).
-
Für
den Fall h
= 0 ist der Differenzenquotient undefiniert. Daher verwenden wir den
Grenzwert für h
→ 0, also den Differentialquotienten f'(1) an der
Stelle x0 = 1.
- Mit Hilfe des Differentialquotienten bekommen wir
also
die Tangentensteigung. Wie man den Differentialquotienten konkret
berechnet, siehst du in der folgenden Anleitung.
|
|
Wir berechnen jetzt den Differentialquotienten
f'(1) für
die Funktion
f(x)
= 2
x2.
Damit bekommen wir die Steigung der Tangente an die Funktion
f(x)
= 2
x2
an
der Stelle
x0 = 1. Vollziehe
alle Schritte nach, indem du jeweils
rechts auf
den blauen Pfeil klickst.
| Laut Definition ist
der Differentialquotient: |
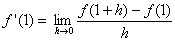 |
▼
|
| in
f
einsetzen: |
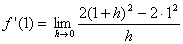 |
▼
|
| Klammer
quadrieren: |
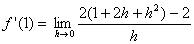 |
▼
|
| Klammer
ausmultiplizieren: |
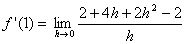 |
▼
|
| h
herausheben: |
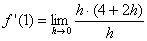 |
▼
|
| durch
h
kürzen: |
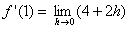 |
▼
|
| Grenzwert
für h
→ 0: |
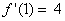 |
▼ |
Lösung: Die Steigung der Tangente an f(x)
= 2
x2
an der Stelle 1 ist 4.
Übung 1b
Bestimme die Steigung der Tangente an
f(x)
= 2
x2
an
der Stelle 2 so wie in Übung 1a in deinem Heft.
Übung 1c
Hier siehst du, wie die Steigung der Tangente an
f(x)
= 2
x2
allgemein für eine Stelle
x0
berechnet wird. Vollziehe alle Schritte dieses Beispiels nach,
indem du jeweils rechts auf
den blauen Pfeil klickst.
| Laut Definition ist
der Differentialquotient: |
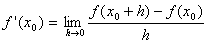 |
▼ |
| in
f einsetzen: |
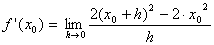 |
▼ |
| Klammer
quadrieren: |
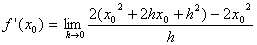 |
▼ |
| Klammer
ausmultiplizieren: |
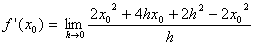 |
▼ |
| zusammenfassen: |
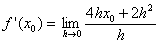 |
▼ |
| h
herausheben: |
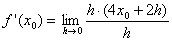 |
▼ |
| kürzen: |
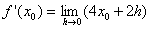 |
▼ |
| Grenzwert
für h
→ 0: |
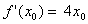 |
▼ |
Lösung:
Die
Steigung der Tangente von f(x)
= 2
x2
für eine gegebene Stelle x0 ist f'(x0)
= 4 x0.
Übung 1d
- Berechne die Steigung der Tangente an f(x) mit Hilfe des
Ergebnisses von Übung 1c an mindestens
drei Stellen in deinem Heft.
- Überprüfe deine Ergebnisse, indem
du im
rechten
Fenster die Stelle x0 mit der Maus
einstellst.
- Hast du in Übung 1b richtig gerechnet?
|
©
M.
Hohenwarter, 2005, erstellt
mit GeoGebra
|